| | Nombres complexes. |  |
|
|
| Auteur | Message |
|---|
Lagalère
milli posteur

Nombre de messages : 58
Classe/Métier (si enseignant, précisez) : Terminale S, spécialité Maths.
Date d'inscription : 26/11/2006
 |  Sujet: Nombres complexes. Sujet: Nombres complexes.  Jeu 11 Oct - 14:05 Jeu 11 Oct - 14:05 | |
| Bonjour, j'éprouve quelques difficultés à résoudre l'exercice ci-dessous:
On considère le polynôme complexe P défini par: P(z)= z^4 - 6z^3 + 24z^2 - 18z + 63.
1/ Calculer P ( i (racine carrée de 3)) et P ( -i(racine carrée de 3)) puis montrer qu'il existe un polynôme complexe Q du second degré à cofficients réels que l'on déterminera tel que, pour tout z appartient C, on ait: P(z)= (z^2 +3)*Q(z).
2/ Résoudre dans C l'équation P(z)=0.
3/ Placer dans le plan complexe les points A, B, C et D d'affixes espectives z(A)= i (racine carrée de 3), z(B)= - i (racine carrée de 3), z(C)= 3+ (2i(racine carrée de 3)) et z(D)= conjugué de z(C) puis démontrer que ces quatre points appartiennent à un même cercle.
4/ On note E le symétrique de D par rapport à O.
a) Ecrire sous forme trigonométrique le quotient ( (z(C)-z(B)) / (z(E)-z(B)) ).
b) En déduire la nature du triangle BEC.
Pour le 1/, j'ai trouvé, par le calcul: P ( i (racine carrée de 3))= 0 et P ( -i(racine carrée de 3))= 0
Les complexes ( i(racine carrée de 3)) et ( -i(racine carrée de 3)) sont donc racines sur le polynôme P.
Ainsi, il existe un polynôme Q du second degré à coefficients réels tels que :
P(z)= (z ( - i (racine carrée de 3)) ) (z ( - i (racine carrée de 3)) ))*Q(z) équivaut à P(z)= (z^2 - ( - i (racine carrée de 3))^2 )*Q(z) équivaut à P(z)= (z^2 +3)*Q(z).
Mais après, je n'arrive plus à continuer.
Je vous remercie de l'aide que vous voudriez bien m'apporter. | |
|
  | |
stardeath
Adminimatheur



Nombre de messages : 1036
Classe/Métier (si enseignant, précisez) : Master 2 informatique
Localisation : bonne question ...
Loisirs : mangas, jeux videos, informatique, coding ...
Date d'inscription : 05/02/2006
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Sam 13 Oct - 18:13 Sam 13 Oct - 18:13 | |
| alors 1/ Q(z) = az² + bz + c puisque Q est de 2nd degré P(z) = (z² + 3)(az² + bz + c) P(z) = az^4 + bz^3 + (3a + c)z² + 3bz + 3c par identification : a = 1 3c = 63 => c = 21 b = -6 3b = -18 => b = -6 3a + c = 24 => 3 * 1 + 21 = 24 => 24 = 24 donc : P(Z) = (z² + 3)(1z² - 6z + 24) 2/ P(Z) = 0 <=> (z² + 3) = 0 ou (1z² - 6z + 24) = 0 (z² + 3) = 0 => z = i 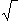 3 ou z = -i 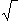 3 (1z² - 6z + 24) = 0, voilà j'ai dégrossi un peu le travail, j'ai un peu la flemme de continuer, si tu as encore besoin hésite pas ^^ | |
|
  | |
Lagalère
milli posteur

Nombre de messages : 58
Classe/Métier (si enseignant, précisez) : Terminale S, spécialité Maths.
Date d'inscription : 26/11/2006
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Jeu 18 Oct - 2:11 Jeu 18 Oct - 2:11 | |
| Pour cela, je vous en remercie. | |
|
  | |
stardeath
Adminimatheur



Nombre de messages : 1036
Classe/Métier (si enseignant, précisez) : Master 2 informatique
Localisation : bonne question ...
Loisirs : mangas, jeux videos, informatique, coding ...
Date d'inscription : 05/02/2006
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Jeu 18 Oct - 16:02 Jeu 18 Oct - 16:02 | |
| | |
|
  | |
Lagalère
milli posteur

Nombre de messages : 58
Classe/Métier (si enseignant, précisez) : Terminale S, spécialité Maths.
Date d'inscription : 26/11/2006
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Jeu 18 Oct - 16:30 Jeu 18 Oct - 16:30 | |
| Oui car le travail a été suffisamment dégrossi^^. | |
|
  | |
stardeath
Adminimatheur



Nombre de messages : 1036
Classe/Métier (si enseignant, précisez) : Master 2 informatique
Localisation : bonne question ...
Loisirs : mangas, jeux videos, informatique, coding ...
Date d'inscription : 05/02/2006
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Jeu 18 Oct - 18:03 Jeu 18 Oct - 18:03 | |
| | |
|
  | |
Shinichi
Adminimatheur



Nombre de messages : 2038
Age : 37
Classe/Métier (si enseignant, précisez) : Maitrise informatique
Localisation : Québec
Loisirs : bcp de choses
Date d'inscription : 04/02/2006
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Sam 20 Oct - 9:41 Sam 20 Oct - 9:41 | |
| D'ailleurs y'a un excellent cours sur ce site sur les nombres complexes !  | |
|
  | |
Lagalère
milli posteur

Nombre de messages : 58
Classe/Métier (si enseignant, précisez) : Terminale S, spécialité Maths.
Date d'inscription : 26/11/2006
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Jeu 29 Nov - 0:32 Jeu 29 Nov - 0:32 | |
| Oui, en effet, c'est ce que j'ai pu constater. | |
|
  | |
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Jeu 29 Nov - 19:59 Jeu 29 Nov - 19:59 | |
| - Shinichi a écrit:
- D'ailleurs y'a un excellent cours sur ce site sur les nombres complexes !
 Ah ?  Ma prof de maths fait mieux  **fait un calin à shinichi qui pleurniche xD** | |
|
  | |
Shinichi
Adminimatheur



Nombre de messages : 2038
Age : 37
Classe/Métier (si enseignant, précisez) : Maitrise informatique
Localisation : Québec
Loisirs : bcp de choses
Date d'inscription : 04/02/2006
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  Dim 9 Déc - 2:10 Dim 9 Déc - 2:10 | |
| T'es sûrE que je pleurniche mademoiselle ? Ah mon avis, t'as mal entendu, je grogne plutot...
:X | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Nombres complexes. Sujet: Re: Nombres complexes.  | |
| |
|
  | |
| | Nombres complexes. |  |
|





