Bonjour! Merci d'avance de votre aide pour cet exercice sur les fonctions :we:
Voici l'exercice :
Soit la courbe (C) ci-dessous, representative de la fonction :
f : x ---> x^3 - 4x + 3, et la droite D d'equation y = -x - 3
1) Resoudre graphiquement l'equation f(x) = 3 puis l'inequation f(x) < 3
f(x) = 3
Les solutions de l'equation f(x) = 3 sont les abscisses des points d'intersection entre (C) et la droite d'equation y = 3
Donc S = {0;4}
f(x) < 3
Les solutions de l'inequation f(x) < 3 sont les abscisses des points de (C) situes strictement en dessous de la droite d'equation y = 3
Donc S = ]-∞;0[ U ]0;4[2) Resoudre graphiquement l'equation f(x) = 0 puis l'inequation f(x) _> 0. On donnera un encadrement d'ampltiude 5 x 10-1 des solutions non entieres.
f(x) = 0
Les solutions de l'equation f(x) = 0 sont les abscisses des points d'intersection entre (C) et l'axe des abscisses
Donc S = {-1;1;3,5]
(Je trouve que ca pourrait egalement etre S = {-1;1;4} ??)
f(x) _> 0
Les solutions de l'inequation f(x) _> 0 sont les abscisses des points de (C) situes sur ou en dessus de l'axe des abscisses
S = [-1;1] U [3,5;+∞[
(Je trouve que ca pourrait egalement etre S = [-1;1] U [4;+∞[ ??)
3) Resoudre graphiquement l'equation f(x) = -x - 3 Puis l'inequation
f(x) _< -x - 3
f(x) = -x - 3
Les solutions de l'equation f(x) = -x - 3 sont les abscisses des points d'intersection entre (C) et D
S = {-1;2;3}
f(x) _< -x - 3
Les solutions de l'inequation f(x) _< -x - 3 sont les abscisses des points de (C) situes sur ou en dessous de D
S = ]-∞;-1] U [2;3]4) Resoudre algebriquement la question 1)
f(x) = 3
x^3 - 4x + 3 = 3
x^3 - 4x = 0
x (x^2 - 4) = 0
x (x-2)(x+2) = 0
x = 0
et x - 2 = 0 x = 2
et x + 2 = 0 x = -2
S = {-2;0;2} (Pourquoi est ce que je trouve Ca??!!)
f(x) < 3
x^3 - 4x + 3 < 3
x^3 - 4 < 0
x (x-2)(x+2) < 0 (Dois - je maintenant faire un tableau de signes?) 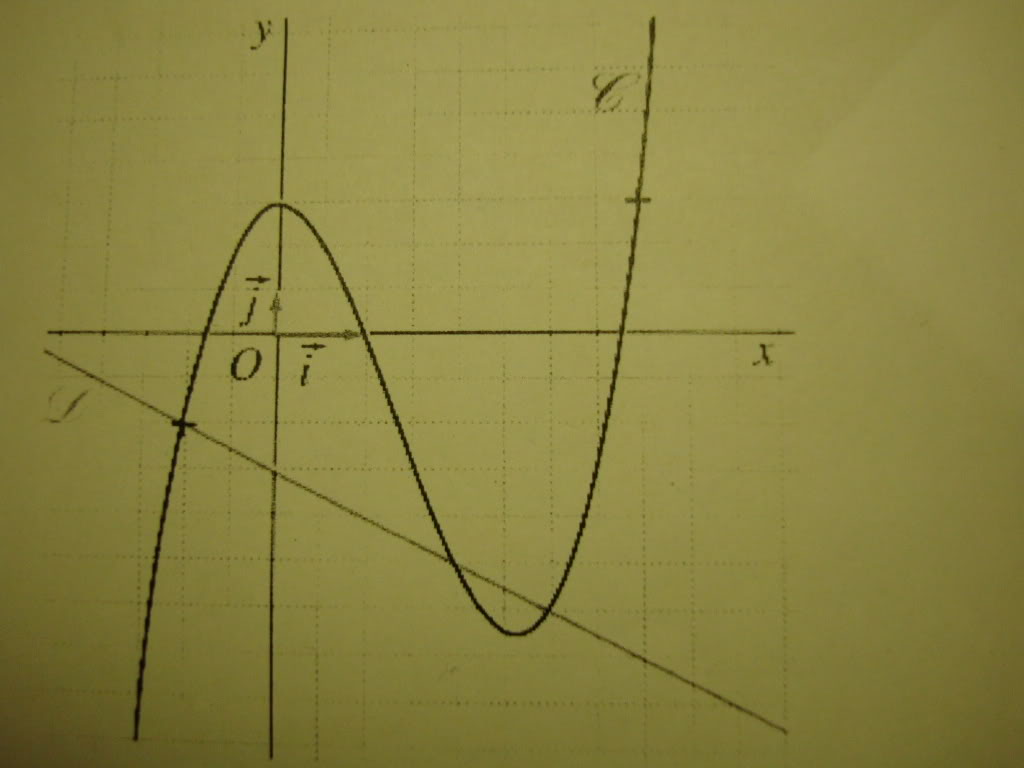
[img][/img][img]





