| | Suite de fonctions |  |
|
|
| Auteur | Message |
|---|
minidiane
bon posteur



Nombre de messages : 191
Age : 37
Date d'inscription : 06/11/2006
 |  Sujet: Suite de fonctions Sujet: Suite de fonctions  Lun 6 Nov - 19:26 Lun 6 Nov - 19:26 | |
| Bonjour j'ai un exercice à faire que je n'arrive pas à résoudre pouvez-vous m'aider?  1) Montrer que fn->0. 2) Montrer que fn->uniformément vers 0 ssi t<1/2. 3) Montrer que fn->uniformément vers 0 sur [0,a] avec 0<a<pi/2. | |
|
  | |
Shinichi
Adminimatheur



Nombre de messages : 2038
Age : 37
Classe/Métier (si enseignant, précisez) : Maitrise informatique
Localisation : Québec
Loisirs : bcp de choses
Date d'inscription : 04/02/2006
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Lun 6 Nov - 20:07 Lun 6 Nov - 20:07 | |
| Par contre, je pense pas d'être d'une grande utilité mais dans les questions, les -> veulent dire tendre ? | |
|
  | |
minidiane
bon posteur



Nombre de messages : 191
Age : 37
Date d'inscription : 06/11/2006
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Lun 6 Nov - 20:21 Lun 6 Nov - 20:21 | |
| Oui c'est cela désolé je ne savais pas trop comment le mettre | |
|
  | |
Shinichi
Adminimatheur



Nombre de messages : 2038
Age : 37
Classe/Métier (si enseignant, précisez) : Maitrise informatique
Localisation : Québec
Loisirs : bcp de choses
Date d'inscription : 04/02/2006
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Lun 6 Nov - 20:43 Lun 6 Nov - 20:43 | |
| c'est vrai que c'est une colle, je vois pas trop comment faire... | |
|
  | |
minidiane
bon posteur



Nombre de messages : 191
Age : 37
Date d'inscription : 06/11/2006
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Lun 6 Nov - 21:03 Lun 6 Nov - 21:03 | |
| | |
|
  | |
St@rguill
Aidematheur



Nombre de messages : 149
Age : 37
Classe/Métier (si enseignant, précisez) : Ecole d'ingénieurs (Matméca-3ième année)
Localisation : Bordeaux (Talence)
Loisirs : Musique, Séries TV, Maths...
Date d'inscription : 10/06/2006
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Mar 7 Nov - 18:21 Mar 7 Nov - 18:21 | |
| Salut, Ca serait bien que tu nous dises à quel chapitre cet exercice correspond. En attendant, il faut peut-être utiliser la définition complèxe du sinus et du cosinus :  et développer tout ça. Je ne sais pas si ça fonctionne, mais j'essairais ce soir. | |
|
  | |
minidiane
bon posteur



Nombre de messages : 191
Age : 37
Date d'inscription : 06/11/2006
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Mar 7 Nov - 20:56 Mar 7 Nov - 20:56 | |
| Le chapitre s'appelle suites de fonctions.
Je vais essayer avec les formules que tu ma rappeller. | |
|
  | |
minidiane
bon posteur



Nombre de messages : 191
Age : 37
Date d'inscription : 06/11/2006
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Lun 11 Déc - 12:35 Lun 11 Déc - 12:35 | |
| Bonjour voilà je suis bloqué sur cet exercice. Soit (fn)n 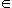 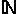 la suite de fonctions définies sur I=[0,2] par fn(x)= x^n/(1+x^n) Montrer que la convergence est unifrome sur toute partie [0,a]U[b,2] avec 0<a<1<b<2. Montrer que lim 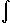 de 0 à 2 de fn(x) dx=1 quand n  + 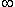 | |
|
  | |
dominique10
nouveau membre

Nombre de messages : 4
Date d'inscription : 22/03/2007
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Jeu 22 Mar - 20:32 Jeu 22 Mar - 20:32 | |
| il faut majorer fn en fait sa valeur absolue par une fonction ou qq chose qui tend vers 0
que faire ?
tu vois que sinp(n) (x) se majore par 1
cos(x) se majore < par 1
donc fn se majore < par np(t) ,n puissance t
np(t) tend vers 0 à la seule condition que t< 0
2) uniformémément veut dire qu'une variable s en va elle disparait
sur [0, pi/2] sin x < 2/pi ,fois x
donc fn se majore par < np(t) ((2/pi) x) puissance n = (1)
je te rappelle que 2 puissance n=exp n log 2
donc (1) < exp (t) log n exp n log (2/pi) x = exp (t) logn + n log (2:pi) x
= exp nlogn ((t)/n + log (2/pi) x /log n ) = (3)
or log 2/pi x < log 1 =0 sur [ 0,pi/2]
(3) < exp n log n ( (t) / n ) = exp log n p(t) =exp (t) log n =
CA MARCHE PAS
SI LA FONCTION DOIT CONVERGER UNIFORMEMENT IL FAUT ENLEVER UE VARIABLE MAIS L AUTRE
np(t) < n p(1/2) pour t dans <1/2
ENSUITE REPRENDRE CE QUI J AI ECRIT AVANT si x dans [0, pi/2]
np(t) sin p(n) x cos x < np(1:2) (2/pi) p(n) ceci tend vers 0 car de la forme npuissance b muliplié par l inverse de a puissance n
avec a compris entre 0 et 1
3) convergence uniforme encore mais sur un intervalle qui contient celui sur lequel on a commencé
donc on majore encore et on majore encore d e la meme manière mais au lieu de 2/ pi c est un autre nombre qui apparait
regarde le schéma de la fonction sinus sur 0 pi/2 prends un intrvalle plus peit que celui là e rejoint le point 00 au point de la courbe qui correspond à celui que tu prends sur 0 pi:2 tu vois que ce point est entre 0 et 1
tu remplaces 2/pi par ce nombre et cela tend encore vers 0 | |
|
  | |
minidiane
bon posteur



Nombre de messages : 191
Age : 37
Date d'inscription : 06/11/2006
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  Sam 24 Mar - 11:29 Sam 24 Mar - 11:29 | |
| Merci pour ton aide dominique | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Suite de fonctions Sujet: Re: Suite de fonctions  | |
| |
|
  | |
| | Suite de fonctions |  |
|





