Espaces métriques

Bonjour tout le monde voilà j'ai deux démonstrations à faire et je n'arrive pas à les faire pouvez-vous m'aider?

Démonstration1: N infini: E ->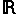
x1associe N infini= max |xi| (avec 1 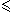i 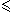n)
Montrer que c'est une norme.


Démonstration2: Montrer que:
dans un espace métrique (E,d) toute sphère S(a,r) est un fermé.

Pour le 1, il faut vérifier tous les axiomes. Pour l'inégalité triangulaire, je ne me souviens plus exactement la démo. Je sais qu'on en déduit l'inégalité de Cauchy-Schwarz...

Pour la deux : il faut untiliser l'image réciproque d'un fermé qui est un fermé. En effet, si tu regardes l'application norme, qui a un vecteur x associe la norme de (x-a), alors la sphère S(a,r) est l'image réciproque de {r}. Tout singleton est un fermé donc la sphère S(a,r) est un fermé.

Merci de ton aide pour la dernière fois je viens de remarqué que je ne t'avais pas remercié st@rguill.

Bonjour tout le monde je n'arrive pas à faire certaines démonstrations pouvez-vous m'aider?

1) Soit E un evn et soit A un sev de E. Montrer que: A ouvert implique A=E
2) Soit E un evn. Soit K un compact de E et F un fermé de E. Montrer que:

i) K+F={x+y: x 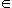K, y 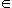F} est fermé.
ii) F compact implique K+F compacte.

Merci de bien vouloir m'aider.