Bonsoir à tous voilà j'ai quelques soucis dans quelques exercices pouvez vous m'aider?
Exercice1:
x= 1 2 3 4 5 6
4 2 6 3 5 1
y= 1 2 3 4 5 6
2 1 3 5 6 4
z= 1 2 3 4 5 6
1 5 3 4 2 6
On me demande quels sont les supports de x, y, z et xrondy et xrondz, je ne sais pas ce que c'est.
Exercice2
On considère le groupe symétrique Sn d'ordre n.
1. Rappeler quel est l'ordre d'un cycme c=(a1, a2, ..., ak) de longeur k où k n.
2. Soient c1 et c2 deux cycles de supports disgoints et d'ordre respectifs m et p. Démontrer que l'ordre de c1c2 est ppcm(m,p).
Exercice3
1. Montrer que les transpositions de type (1,i) 2
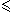
i
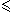
n-1 engendrent Sn.
2. Montrer que les transpositions du type (i,i+1) 1
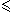
i
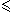
n-1 engendrent Sn.
3. Montrer que (1,2) et (1,2,...,n) engendrent Sn.
Exercice4
Soient G={Id, (1,2)rond(3,4), (1,3)rond(2,4), (1,4)rond(2,3)} et H={Id, (1,2,3,4), (1.3)rond(2,4), (1,4,3,2)}
1. Démontrer que G et H sont des sous-groupes de S4.
2. Soit f un morphisme de groupes de G dans H. Montrer que pour tout s G, (f(d))²=id.
3. En déduire que les groupes G et H ne sont pas isomorphes.





