Dérivé en géométrie

Bonjour,

J'ai un exo de maths, ou je ne comprends rien, enfin pas grand chose :/
voici :

ABCD est un carréde côté 10cm. Pour tout point M de [AB], on nomme I le point d'intersection de [DM] et [AC], x la longueur AM, et A(x) l'aire totale des deux triangles AMI e DIC.

1) Calculer 1(0) et A(10)

2) Montrer que si x 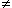0, les triangles AMI et CDI sont semblables.

3) Soit h la hauteur issue de I dans le triangle AMI. Montrer que
h/10-h = x/10 puis que h = 10x/10+x

4) Montrer que A(x) = 5(x²+100)/x+10 sur [0;10]

5) Etudier le sens de variation de A et en déduire la position de M assurant une aire totale minimaum.



Merci d'avance.

Snif, vous avez pas une petite idée ?

Salut !

1) 1(0) : c'est quoi, A(0) ? Si c'est le cas, alors on a le carré coupé en 2 triangles rectangles, donc l'aire c'est la moitié du carré, soit 50cm²

A(10), x=10, donc en fait, ton carré est découpé en 4 triangles rectanges. Donc l'aire en jaune c'est la moitié de l'aire totale du carré, soit 10²/2 = 50 cm²

2) Je pense qu'ici il faut utiliser les angles alternes/internes et angle au centre. Tu as l'angle en I qui ne varie pas, on a aussi angle(BAI) = angle(ICD) (du moins en valeurs en degrés) et Idem pour D et M, donc les triangles sont semblables.

Voilà déjà le début, je te laisse continuer