Aubrac
micro posteur
Nombre de messages : 10
Age : 33
Classe/Métier (si enseignant, précisez) : 1ére S
Localisation : Ici
Loisirs : Musique
Date d'inscription : 22/09/2007
 |  Sujet: problème d'équation  Jeu 3 Jan - 13:42 | |
| Bonjour , j'ai une equation , mais je ne comprend pas comment on peut la résoudre ,
f(x)x^3+x²-2x=0
Voila , merci d'avance , si vous pouvez me donner un coup de main | |
|
Nakonjo
Aidematheur
Nombre de messages : 388
Age : 34
Classe/Métier (si enseignant, précisez) : PC
Localisation : Entre la Pierre et L'eau
Loisirs : Musique, programmation, physique
Date d'inscription : 03/05/2007
| | Sujet: Re: problème d'équation Jeu 3 Jan - 14:06 | |
| Ton équation c'est x^3+x^2-2x = 0 ? Bon on va dire que c'est ça ^^ Un petit coup de main ? C'est tout bête, tu as juste à factoriser ton expression par x, et après comme tu connais les polynômes de second degré (enfin je suppose  ^^), tu trouves facilement la solution  Si jamais, tu ne trouves vraiment pas, ou que tu veux juste avoir la certitude que c'est ça [bien que je puisse faire des fautes  , je suis pas prof^^] : - Spoiler:
x^3+x^2-2x = 0 <=> x.(x^2+x-2) = 0 <=> soit x = 0 ; soit (x^2+x-2) = 0 On va donc chercher le discriminant 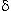 = b² - 4ac = 1 + 8 = 9 Les deux racines sont donc X1 = 1 et X2 = -2 Du coup les solutions de l'équation x^3+x^2-2x = 0 sont S={-2;0;1} .
| |
|
Aubrac
micro posteur
Nombre de messages : 10
Age : 33
Classe/Métier (si enseignant, précisez) : 1ére S
Localisation : Ici
Loisirs : Musique
Date d'inscription : 22/09/2007
| | Sujet: Re: problème d'équation Jeu 3 Jan - 17:22 | |
| OK merci , je viens de regarder le spoiler , et ça correspond a mes resultats .
Merci de m'avoir aider | |
|
Contenu sponsorisé
| | Sujet: Re: problème d'équation | |
| |
|
