calcule d'integrale

bonjour a tous
je voudrait savoir si mes reponses sont justes.


pour tout n entier naturel
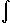
In= 0 ^ (x-1)sin(nx) dx

1. calculer In en fonction de n

moi j'ai fait :
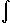
In= 0 (x-1)sin(nx) dx

u'=sin(nx) u= -(1/n)cos(nx)
v=x-1 v'= 1

In= [(x-1)*((-1/n)cos(nx))]- 0:integrale:^ -(1/n)cos(nx) dx

(je passe des etapes)
In = (-1)(-(1/n)cos(nx))+ 1/n² sin(nx)

mais la je n'arrive pas a expliquer que n:pi:= 0 ou :pi:donc sin(nx) = 0 pour tt n entier naturel

et donc In= (-1)(-(1/n)cos(nx))


2. La suite est elle convergente ?

je fais un encadrement de cos x. Est ce que c'est juste ?

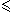
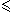
ca me donne -1 cos(n:pi:) 1

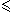
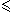
1/n 1/n cos(n:pi:) -1/n

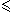
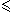
-1/n -1/ncos(n:pi:) 1/n

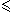
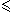
(-1)(-1/n) (-1)(-1/n cos (:pi:n)) (-1)(1/n)

(quels sont les explication que je dois obligatoirement mettre en chaque etapes ??)

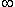
donc lim n:fleche:+(-1)(1/n)=0

car lim n:fleche:+:infini:1/n = 0
idem pour lim de ]-(-1)(1/n)

donc d'apres le theorem des gendarmes lim ](-1)(-1/n cos(:pi:n))= 0

donc la suite converge vers 0


est ce que c'est juste ???

MErci d'avance pour votre aide !

je ne suis juste pas d'accord au niveau du sens des inégalité dans la question 2

on a bien -1 <= cos (n*pi) <= 1
mais pour diviser par n, vu que n est un entier naturel (il faut deja le supposer différent de zero), tu n'as pas besoin de changer le signe de l'inégalité.

Je ne pense pas que cela fausse le résultat pour autant.

bonjour
en supposant que l'écriture 0 ^ veut dire "l'intégrale de 0 à " on trouve
In = (1-)cos(n:pi:)/n- 1/n + sin(n:pi:)/(n*n)
on voit que pour tout n, sin(n:pi:)=0
donc si n pair In = -/n
si n impair In = (-2)/n