| | équation à 2 inconnues |  |
|
|
| Auteur | Message |
|---|
mimou
micro posteur

Nombre de messages : 11
Classe/Métier (si enseignant, précisez) : première S
Date d'inscription : 13/05/2008
 |  Sujet: équation à 2 inconnues Sujet: équation à 2 inconnues  Dim 19 Oct - 20:16 Dim 19 Oct - 20:16 | |
| coucou !  je suis en terminal mais je suis bloquées sur cette équation 2y+6x+5=0  si vous pouviez me donner un ti coups de pouce !! | |
|
  | |
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Re: équation à 2 inconnues Sujet: Re: équation à 2 inconnues  Dim 19 Oct - 22:57 Dim 19 Oct - 22:57 | |
| Euh, c'est au programme de spé non ?
Si mes souvenirs sont bon, il faut d'abord résoudre 2y+6x=0 et ensuite 2y+6x=-5 mais alors pour le reste... | |
|
  | |
Shinichi
Adminimatheur



Nombre de messages : 2038
Age : 37
Classe/Métier (si enseignant, précisez) : Maitrise informatique
Localisation : Québec
Loisirs : bcp de choses
Date d'inscription : 04/02/2006
 |  Sujet: Re: équation à 2 inconnues Sujet: Re: équation à 2 inconnues  Lun 20 Oct - 2:18 Lun 20 Oct - 2:18 | |
| Non non Eximma. C'est du programme de spé mais y'a pas une seule solution forcément vu que t'as 2 inconnues pour une seule équation. Ca fait parties des équations diophantiennes (je crois, si mes souvenirs sont bons). Ce que tu peux faire, c'est exprimer x en fonction de y.
Ensuite tu trouves les entiers pour les lesquels y et x sont entiers.
PS : vu la tete de l'équation, je suis parti du principe que x et y était entier. C'est le cas ? Sinon ben il y a une infinité de solutions.
Dernière édition par Shinichi le Mar 21 Oct - 3:08, édité 1 fois | |
|
  | |
R.O.G
Aidematheur



Nombre de messages : 471
Age : 36
Classe/Métier (si enseignant, précisez) : Professeur (stagiaire)
Localisation : Rennes
Loisirs : Sports d'endurance
Date d'inscription : 22/02/2008
 |  Sujet: Re: équation à 2 inconnues Sujet: Re: équation à 2 inconnues  Lun 20 Oct - 14:04 Lun 20 Oct - 14:04 | |
| Bonjour.
S'il s'agit d'une équation diophantienne (dans ZxZ), elle n'a pas de solution. (Pourquoi ?)
Mais, faut-il la résoudre dans ZxZ ?
Voilà. | |
|
  | |
Redola
hyper posteur


Nombre de messages : 315
Age : 41
Classe/Métier (si enseignant, précisez) : ingénieur
Localisation : Lille
Date d'inscription : 28/09/2006
 |  Sujet: Re: équation à 2 inconnues Sujet: Re: équation à 2 inconnues  Lun 20 Oct - 18:43 Lun 20 Oct - 18:43 | |
| Dans Z, pas de solution ^^ (somme de deux nombres pairs ne peut être impaire) (méthode qui ne marche aps dans tous les cas...)
Sinon, le théorème de bezout te permets de conclure sur la non existence de solution dans ZxZ | |
|
  | |
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Re: équation à 2 inconnues Sujet: Re: équation à 2 inconnues  Lun 20 Oct - 22:00 Lun 20 Oct - 22:00 | |
| - Redola a écrit:
- Sinon, le théorème de bezout te permets de conclure sur la non existence de solution dans ZxZ
Ahhh merci pour le nom, j'l'avais oublié (Honte à moi je sais  ) | |
|
  | |
stardeath
Adminimatheur



Nombre de messages : 1036
Classe/Métier (si enseignant, précisez) : Master 2 informatique
Localisation : bonne question ...
Loisirs : mangas, jeux videos, informatique, coding ...
Date d'inscription : 05/02/2006
 |  Sujet: Re: équation à 2 inconnues Sujet: Re: équation à 2 inconnues  Lun 20 Oct - 22:06 Lun 20 Oct - 22:06 | |
| ayant 2 inconnus, cette équation se traite forcément dans un ensemble du type : ensemble 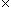 ensemble, c'est obligatoire. le reste c'est de l'abus de langage. dans 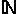 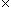 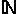 : impossible, la somme d'entiers strictement positifs ne peut être = 0 dans Z 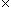 Z (à rajouter dans les icônes d'ailleurs) : impossible, on peut obtenir y = (-6x - 5) / 2 hors 6x,  x 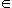 Z est pair et la somme un entier relatif pair et d'un entier relatif impaire est forcément impaire. dans les ensembles 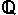 , 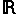 et 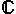 , il y a une infinité de solutions (si je me goure pas) | |
|
  | |
Shinichi
Adminimatheur



Nombre de messages : 2038
Age : 37
Classe/Métier (si enseignant, précisez) : Maitrise informatique
Localisation : Québec
Loisirs : bcp de choses
Date d'inscription : 04/02/2006
 |  Sujet: Re: équation à 2 inconnues Sujet: Re: équation à 2 inconnues  Mar 21 Oct - 3:07 Mar 21 Oct - 3:07 | |
| ROG diophantienne c'est le mot oui.  J'ai confondu et édité mon post donc.  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: équation à 2 inconnues Sujet: Re: équation à 2 inconnues  | |
| |
|
  | |
| | équation à 2 inconnues |  |
|





