raisonnement par récurrence

Bonjour, voila jai un probleme avec ces 2 exercices sur les suites!!
J aimerai bien avoir de laide pq c urgent merci davance a ts!!
On definit la suite u par u(indice 0)=2 et u n+1=racine de u(indice n)pour tout n superieur ou egal a 0.
Montrer que la suite est bornee par 1 et 2.

et mon 2eme exercice est encore plus dur
Comparer 2 indice n et n puissance 2 pour differentes valeurs de n.
Resoudre l'inequation 2n puissance 2 superieur ou egal a (n+1)au carré.
Demontrer par recurence que pour tout n superieur a 3, 2 puissance n superieur ou egal a n au carre.
Pour quelles valeurs de n a t on 2 puissance n superieur ou egal a n puissance 2?

merci merci bcp!!!

Pour la suite u(n+1)= u(n), il faut calculer quelques valeurs de un pour n=1..3. On s'apperçoit alors du comportement supposée de la suite.
Pour savoir si la suite est croissante ou décroissante, il faut calculer u(n+1) - u(n) ou calculer u(n+1)/u(n).
Ensuite, je ne sais plus si on le voit en terminale, mais tu peux trouver la limite de la suite avec un graphique ( f(x)=x et f(x)= x ) et en utilisant plusieurs résultats connus (la limite, si elle existe, vérifie l= l )

Pour le deuxième exercice, je ne comprends pas le "2 indice n" !

J'espère que mon aide te sera utile

merci bcp de ton aide!!! quand au deuxieme exercice cest 2 puissance n en fait !!!

_|2^n|n²
0| 1 |0
1| 2 |1
2| 4 |4
3| 8 |9
4| 16 |16
5| 32 |25
6| 64 |36
7|128|49
----------------------------------------------------------------------
2n² >= (n+1)²
2n² >= n² + 2n + 1
n² - 2n - 1 >= 0

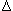
= b² - 4ac = 8

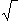
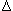
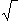
r = (2 ) / 2a = 1 2
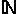
comme on travaille dans on élimine la valeur négative on garde r = 2,41... donc r = 3

donc 2n² >= (n+1)² pour tout n >= 3
-----------------------------------------------------------------------
récurrence :

init:
n = 4 : 2^4 = 16 4² = 16
donc 2^n >= n² pour n=4

hypothèse de récurrence :
2^n >= n² vrai pour tout n>=4

démontrons le à n+1 :
2^(n+1) >= (n+1)² ???

d'après l'hyp de réc nous avons:
2^n >= n² pour n>=4
2*2^n >= 2*n² pour n>=4
2^(n+1) >= 2n² pour n>=4

nous savons aussi que :
2n² >= (n+1)² pour tout n>3

donc :
2^(n+1) >= 2n² >= (n+1)² pour tout n>=4
donc hyp de réc vrai à l'init, pour n>4, pour n+1, n>=4 donc vrai pour tout n>=4
finalement : 2^n >= n² pour tout n>=4

^^

merci bcp c tre gentil ms est ce que vous pouriez maider pr montrer que la suite est bornee ds lexercice 1 pq je bloque vraiment la!!!
encore merci pr lexercice 2!!!!!!!!