question de math

bonjour, voila l'ennoncé:
1. En choisissant convenablement les uintés sur les axes représentez sur l'intervalle ]0 ; 40] les fonctions suivantes: f : x->1/x et g : x->x (/ représentant sur. exemple 1/2=1sur2)

2. Quel semble être le nombre de points d'intersection des deux courbes? Calculez leurs coordonnées exactes.

Voila, ma prof elle a fait le cour d'une traite, et trop rapidement, donc j'ai rien compris, merci de répondre avant jeudi
merci

Bon, alors pour le dessin, je vais avoir un peu de mal à te le passer

Mais je vais te donner la méthode :

La fonction f est définie par f : x 1/x, elle tu connais sa représentation graphique par coeur [] => C'est une hyperbole Tu sais le truc bizar :

Et puis g : x x t'as pas le droit que tu ne la connais pas C'est une droite qui passe par O [l'origine du repère] et qui pour chaque x gagné, gagne un y [en fait y = x] Bon je te mets une petite représentation parce que je suis de bonne humeur :

Tu devrais donc obtenir au final quelque chose dans ce genre [excuse moi, c'est pas top, mais bon, c'est mieux que rien ] :


Voila pour le 1°), passons au 2°) maintenant :
Tu vois qu'il y a donc apparement deux points d'intersections en (-1 ; -1) et en (1 ; 1) et si tu y réfléchi, tu te rends compte que c'est tout à fait logique

Bon bin maintenant un peu d'algèbre :
On veut que les deux courbes se coupent, ça veut donc dire que leur abscisse est la même et que leur ordonnée est aussi la même
Du coup, on peut poser une équation : f(x) = g(x), on va donc chercher x tel que f(x) = g(x) [j'ai l'impression de me répéter là c'est normal ?]
Or tu sais que f(x) = 1/x et que g(x)=x, on peut donc mettre :
1/x = x // Maintenant, je multiplie à gauche et à droite par x
1/1 = x² // Maintenant je fais une simplification de fraction super compliquée
1 = x² Du coup tu cherche les racines, qui sont... ... ... Pourquoi tu dis les racines, il n'y a que 1 vu que 1x1 = 1 donc 1² = 1 !? Et -1 tu en fais quoi ? (-1)x(-1) = 1 ! Donc (-1)² = 1 donc x² = 1 a deux solutions !
S = {-1 ; 1}
Bon du coup maintenant, on a les abscisses [les "x"], on va chercher l'ordonnée [les "y"] de ces points... Et j'ai une fonction qui s'y prête mieux que l'autre, c'est g(x) ! g(x) = x on a donc une fonction telle que y = x [si tu pige pas, tu me demande, il n'y a rien de compliquer, mais je ne m'éternise pas dessus ] donc les ordonnées sont les même que les abscisses, c'est de cette manière que je trouve que les courbes de f et de g se coupent en A (-1 ; -1) et en B (1 ; 1)

Voila, j'éspère avoir correctement répondu à ta question

les axes représenté sur l'interval ]0;40], il nous sert a rien comme information alors???

Pour etre frant; j'ai pas tous compris (pour ne pas dire rien), c'est chaud quand meme, mais je vais recopier, et j'essairais de comprendre en cour!
merci pour ta réponse (Tu doit etre fort en math quand meme!!! Tu répond a tout!)

Euh en fait on peut pas dire que je sois super fort en maths, mais bon je suis en 1ère du coup, bin je dois bien connaître le programe de seconde parce qu'on utilise tout les jours d'anciens trucs

J'ai fait une grosse faute tu as raison dans ma première question, je n'ai pas pris en compte l'information que l'on travaillait sur ]0 ; 40]

Bon, comme tu n'as pas compris, je vais tout te réexpliquer [c'est mieux de comprendre quand même un minimum avant le cour, ça permet de ne pas être largué le jour du devoir ] [ne te vexe pas, comme je ne sais pas trop ce que tu n'as pas compris, je vais tout t'expliquer, quasiment comme si tu n'avais jamais fait de maths ] :

1°) Bon alors là on te demande de représenter graphiquement tes fonctions. Qu'est-ce qu'une représentation graphique ? C'est tout simplement l'allure qu'a ta fonction sur un graphique [ça tu dois le savoir quand même, nan ? ]

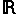
On va donc commencer par la fonction g qui est la plus simple. Tout d'abord on sait que g est une fonction linéaire [de la forme f : x ax avec a appartenant à ] Bon, on a de la chance, c'est la fonction la plus simple que tu puisse jamais rencontrer Bin c'est facile [enfin je dis ça parce que je sais ^^ ], tu vas voir :
g(x) = x
g(x) c'est quoi en fait ? Bin c'est l'ordonnée y qui est associée au point qui a comme abscisse x [j'éspère que tu me suis, parce que ça va se corser tout à l'heure je pense ^^ ]
On a donc g(x)=y donc [et tout à fait logiquement] y=x
Donc tous les points de la courbe qui a comme équation g [on peut aussi dire la courbe représentative de la fonction g] ont comme ordonnée la même que leur abscisse. Quoi de plus simple pour nous ? Bin rien je crois ... ... ...


Excusez-moi j'ai eu la fleme de l'héberger...

Bon bin voila la représentation graphique de g... Comment tu la fais ? Bin comme g est une fonction linéaire, bin tu sais que c'est une droite qui passe par l'origine du repère O (0 ; 0) et par un autre point dont on calcul les coordonnées tout de suite, aller bon être original A (1 ; 1) et pour te rassurer B (10 ; 10)... Si t'as pas compris là, dis le moi parce qu'il faut absolument que tu sache ça en 2nde !

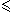
En effet dans l'énoncé on te parle d'intervalle ]0 ; 40], du coup, bin tu dois représenter ta fonction pour 0 < x 40 [comme tu l'as compris, aussi pour 0 < y < 40 - comme y = x ^^ - ]

Bon, on passe à la fonction f ^^ Comme on est sur ]0 ; 40] ça va être plus facile [si tu te demande pourquoi, calcule f(0) ]
On va calculer 5 valeurs pour te remémorer l'allure de la courbe [parce que je suis sur que tu l'as vu en classe ] Ce qu'on va faire c'est que je t'en demande plusieurs, je te donne la correction un peu en bas [comme ça il n'y pas que moi qui bosse ici ]
Pour x=1/4
Pour x=1/2
Pour x=1
Pour x=2
Et pour finir x=4

Voila les réponses : [il faut que tu clik sur Spoiler ^^ Je te dis ça parce que moi je me suis fait avoir la première fois ]

Spoiler:

Bref, c'est cool, on a des points, mais maintenant on fais quoi avec ? Bin on les dessine sur son brouillon [c'est un virus que m'a passé ma prof de maths, l'utilisation d'un brouillon ] Et après essaye de tracer une courbe qui les relie tous... Maintenant les cours du début de l'année [je te dis début comme j'aurais pu dire milieu ] remontent à la surface, et *** PAF *** te souviens de l'allure de la courbe de la fonction inverse ^^ [tu sais le truc qu'on appelle hyperbole ^^] et qui ressemble à ça :



Mais là comme on travaille sur ]0 ; 40], bin on ne la représente que sur ]0 ; 40] pour faire simple, tu fais la courbe sur l'autre dessin ^^ et ne te tracasse pas pour les points, tu fais simplement C (1 ; 1) puis comme tu connais l'allure de la courbe, bin tu la refais avec tes souvenirs

Du coup tu dois normalement avoir un dessin qui ressemble à ça [en plus grand, ou en tout cas avec des échelles plus grandes parce que moi les x et les y s'arrêtent pour valeur 5 ^^] :



En fait j'éspère que tu avais déja compris toute la première question, mais je te l'ai réexpliqué parce qu'on ne sait jamais Bon on va passer à la deuxième question maintenant [oui, je sais tu viens de te manger un gros paté dans les dents là ^^ Mais imagine toi que j'ai écris ce paté spécialement pour toi ]


2°) Nous voila enfin ^^

On nous demande les points d'intersection des deux courbes... Tu en vois toi ? Moi oui, j'en vois 1 [normalement il y en a deux si tu réfléchis bien, mais comme on travail sur ]0 ; 40], bin il n'y en a qu'un - et ui j'ai fait une faute dans mon premier message ]

Pour que les deux droites se croisent, il faut que point appartienne en même temps à Cf [la courbe représentative de f] et à Cg [la courbe représentative de g], du coup on va chercher les coordonnées de ce point... Comment on va s'y prendre ? Tu connais les équations ? Bin voila , on a notre méthode :

Pour que f et g se croisent, il faut que f(x) = g(x) [si tu ne comprends pas dis-le ]... Donc on va chercher toutes les valeurs pour lesquelles c'est vrai

Je sais que f(x) = 1/x et que g(x) = x, on a donc : 1/x = x on cherche les valeurs pour lesquelles c'est vrai...
Petit résolution d'équation
1/x = x // Je multiplie à gauche et à droite par x
1 = x² // On va donc chercher les racines de x² telles qu'elles soient égales à 1
On trouve 1 et (-1) [ui, moi aussi je l'oubliai tout le temps avant, c'est normal ], mais comme nous travaillons sur l'intervalle ]0 ; 40], seul 1 nous interesse.

Bon on connait maintenant la valeur de x pour laquelle f et g se croisent, on va donc chercher la valeur de y pour laquelle f et g se croisent. Comme on connait le x en question et la forme de nos fonctions on hésite pas :
f(1) = 1 et g(1) = 1, on trouve comme ça notre ordonnée pour lequel les deux courbes se croisent, et en même temps on vérifie si on a pas fait d'erreur [elle est pas belle la vie ? 8) ]

Comme ça on sait que les courbes représentatives de f et g se croisent au point D de coordonnées D (1 ; 1) sur ]0 ; 40]

En ésperant t'avoir un peu plus aidé, dans le cas où tu aurais des questions n'hésite pas Mais essaye juste de me guider un peu

J'aurais été prof de maths je t'aurais mis 20/20, y a pas mieux comme explication !!!!!!!!! nan sincérement, elle est clair et précise.

Merci, merci, merci C'était mon but [pas d'avoir 20/20, que mon explication soit compréhensible ]

merci pour ta réponse extrement impressionante!
Mais mon prof de math ma expliqué le cour aujourd'hui, et j'ai compris
J'ai une question, t'a mis combien de temps a faire cette réponse???
Sur le coup, je suis impressionné

Nakonjo rougit ^^

Arrêtez ^^, je ne fais que répondre à ta question [avec beaucoup d'explications certes, mais simples ]

Mais bon, le principal c'est que tu ais compris ...

Combien de temps j'ai mis ? Hmm je dirai environ 1 heure, mais comme je faisais plein d'autres trucs en même temps [4 autres forums, msn, révisions de maths, et puis un truc de programmation ^^], je pense que j'aurais mis environ 20 minutes pour tout t'expliquer ... Mais ce qui est important, c'est pas ce que je fais moi, c'est ce que tu comprends toi !

tu devrais etre prophètes!!!!
On dirais robin des bois, t'aide les povres!

Lol, mais arrêterrr !!!

Si je suis sur ce forum, c'est soit pour poser des questions, soit pour y répondre, or en l'occurence, en ce moment, j'ai pas beaucoup de question à poser, donc je réponds à celle que je peux, et ou les gens sont sympa et ou j'aime bien la matière