défi N° 1 2nde

Ce défi est a faire par les seconde, si vous êtes d'un niveau suppérieur, envoyez votre réponse par e-mail.

Exercice 1 : Les ensembles de nombre.

Donnez les différents ensembles de nombre en ordre croissant en donnant un exemple dans chaque ensemble.

Exercice 2 : résolution d'équation.

Résoudre dans IR les équations :

a) (2x+1)²=(2x+1)(1-x)
b) 9x²-(x+2)²=0

Exercice 3 : compléter les phrases.

c) f(x) = g(x) : Les solutions sont......
d) f(x) > 0 : Les solutions sont......
e) f(x) > k* : Les solutions sont.....

*k est un nombre quelquonque

bon courrage

Si je peux juste mettre mon grain de sel, précise quelles sont les variables quand tu dis "les solutions de f(x)=g(x) sont..." car f(x)=g(x) peut très bien être elle même une solution.
Pour l'exo 1, qu'entends tu par ensemble de nombre dans l'ordre croissant?
sinon c'est intéressant.

Pour les ensembles de nombres, comme on veu !

Par exemple : IR : exemple : pi

Pour f(x)=g(x), je voulait juste que l'on complete le phrase :

Les solutions sont les points d'intersections des courbes !

D'autres réclamations ?

non non
mais si je peux ajouter quelque chose, les intersections ne sont pas des solutions. Si la varible est x alors on attend x=..., si tu précise pas quelle est la varible, c'est comme si tu écrivais 4=3+1.
Mais rassure toi, ton programme ne prévoit pas que tu saches bien distinguer toutes ces subtilité car c'est difficile qu'en on en a pas l'habitude.

Pour le b) =====> T'utilise l'identité remarquable : a2 - b2 = (a+b)(a-b)
9x2 - (x+2)2 = 0
(9x+x+2)(9x-(x+2)) = 0
(10x+2)(8x-2)=0
80x2 - 20x + 16x - 4 =0
80x2 -4x-4 =0
10x2 - 1x=-1

Là un peu coincé[/strike]

tu t'es trompé car c'est 9x² et non pas (9x)² donc 9x²=(3x)²
(3x)² - (x+2)² = 0
(3x+x+2)(3x-(x+2)) = 0
(4x+2)(2x-2)=0
A partir d'ici, c'est bidon...^^Regardez le post de Sheppard plus bas.
C'est néanmoins une technique classique utilisée avec les polynomes (ce qui suit).
8x² - 4x - 4 =0
8x² -4x -4 =0
2x² -x -1=0 (A)
et on remarque que 1 est solution donc si on note b la deuxieme solution, on a 2(x-1)(x-b)=0 c'est à dire 2x² (-2b-2)x +2b=0 puis on identifie les coeef de cette équation avec ceux en (A) et on a -2b-2=-1 et 2b=-1 donc b=-1/2

Finalement on a les deux solutions qui sont 1 et -1/2.

Shinichi t'es pas en seconde -_-'

non mais je réponds pas je donne de l'aide

Fl_0RI@/\/ 54 a écrit:

Shinichi t'es pas en seconde -_-'

effectivement, les personne au dessus du niveau seconde NE DOIVENT PAS répondre, mais peuvent naturellement aider, la c'est ce qu'a fait Shinichi4 en disant la fin de la réponse, même s'il est sur qu'il aurait été mieux que ce soit un seconde qui aide

par contre j'ai l'impression que les balises ne marchent pas...

oui, je sas pas pourquoi ^^

bonjour alors moi pour le b) je ferai cela :
on utilise d'abord l'identité remarquable
a² - b²=(a-b)(a+b)

9x²-(x+2)²=0
(3x)²-(x+2)² =0
(3x-(x+2)) (3x+(x+2)) =0
(3x-x-2)(3x+x+2)=0
(2x-2)(4x+2)=0
Un produit de facteur est nul si au moins l'un de ses facteurs est nul alors :

2x-2=0 et 4x+2=0
2x=2 4x=-2
x=2/2 x=-2/4
x=1 x=-1/2

Les solution de l'équation sont x=1 et x=-1/2

Oui c'est vrai, j'ai développé pour rien. Bonne remarque^^
Par contre,

Sheppard a écrit:

Un produit de facteur est nul si au moins l'un de ses facteurs est nul alors :

2x-2=0 et 4x+2=0

C'est pas et mais ou...puisque c'est l'un ou l'autre nul, par forcément les deux.

Bonjour
Pour la b) je ferais cela:

(2x+1)²=(2x+1)(1-x)

(2x+1)(2x+1)=(2x+1)(1-x)
(2x+1)=((2x+1)(1-x))/(2x+1)
2x+1=1-x
3x=0
x=0

Voila ce que j'aurais fait
SALUT

Ca m'a l'air tout a fait juste, Sheppard. Tu aurais pu rajouter à la deuxième ligne de ton développement que x 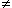-1/2