Lagalère
milli posteur

Nombre de messages : 58
Classe/Métier (si enseignant, précisez) : Terminale S, spécialité Maths.
Date d'inscription : 26/11/2006
 |  Sujet: QCM sur les suites. Sujet: QCM sur les suites.  Jeu 13 Mar - 3:00 Jeu 13 Mar - 3:00 | |
| Bonjour, je voudrais, si c'est possible, avoir une correction de ce QCM, sachant que les trois questions suivantes sont indépendantes et que, pour chaque question, il y a exactement deux propositions correctes:
1/ On considère trois suites (u(n)), (v(n)), (w(n)) ayant, pour tout entier naturel n, les propriétés suivantes: u(n) _< v(n) _< w(n), lim u(n) quand n tend vers +infini = -1 et lim w(n) quand n tend vers +infini = 1. Alors:
a) lim v(n) quand n tend vers +infini = 0.
b) La suite v(n) est minorée.
c) Pour tout n appartient N, on a: -1 _< v(n) _< 1.
d) On ne sait pas dire si la suite (v(n)) a une limite ou non.
2/ Une suite (u(n)) est définie sur N par: {u(0) = 1,5 et u(n+1) = 2u(n) -1.
a) La suite (u(n)) converge vers 1, abscisse du point d'intersection des droites d'équation y = x et y = 2x -1.
b) La suite (v(n)), définie sur N par v(n) = u(n) -1, est géométrique.
c) La suite (v(n)) est majorée.
d) La suite (w(n)), définie sur N par w(n) = ln (u(n) -1) est arithmétique.
3/ La suite (u(n)) est définie, pour tout n appartient N, par: u(n) = 1 + 1/2 + 1/(2)² + ... + 1/(2)^n.
a) La suite (u(n)) est arithmétique.
b) La suite (u(n)) est la somme de termes consécutifs d'une suite géométrique.
c) Pour tout n appartient N, u(n) = 2 - 1/(2)^n.
d) Pour tout n appartient N, u(n) = (n + 1)(1 + 1/(2)^n).
Je vous remercie pour l'aide que vous voudriez bien m'apporter.
P.S.: Mes propositions sont en rouges. | |
|
R.O.G
Aidematheur



Nombre de messages : 471
Age : 36
Classe/Métier (si enseignant, précisez) : Professeur (stagiaire)
Localisation : Rennes
Loisirs : Sports d'endurance
Date d'inscription : 22/02/2008
 |  Sujet: Re: QCM sur les suites. Sujet: Re: QCM sur les suites.  Jeu 13 Mar - 9:36 Jeu 13 Mar - 9:36 | |
| Bonjour. Je ne suis pas convaincu par toutes tes réponses. 1)a) Si on prend un=-1, vn=1/2, wn=1 (  n 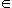 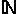 ), on a bien un 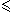 vn 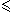 wn et les limites de un et wn comme dans l'énoncé. Mais lim vn 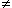 0... c) Il y également un contre-exemple. On prend un=-1-1/(n+1) et wn=1+1/(n+1) Ici u0=-2 et w0=2... 2)b) ok d) ok
3)b) ok c) Essaie de vérifier que c'est vrai en utilisant la formule de la somme des termes d'une suite géométrique. d) Euh non... En conclusion : Mes réponses : - Spoiler:
1) b) d)
2) b) d)
3) b) c)
Voilà ! | |
|





