| | suite definie par une integrale |  |
|
|
| Auteur | Message |
|---|
lachite
micro posteur

Nombre de messages : 25
Classe/Métier (si enseignant, précisez) : classe préparatoire PCSI
Date d'inscription : 31/10/2007
 |  Sujet: suite definie par une integrale Sujet: suite definie par une integrale  Mar 18 Mar - 14:33 Mar 18 Mar - 14:33 | |
| bonjour j'ai un exercice sur les intégrations. Je voudrais savoir si ma premiere reponse est juste et que l'on m'aide pour les questions suivantes car je bloque ^^ On pose In= 1 /(2^(n+1) 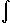 4n  a  (xcos(x/2)) dx 1. calculer I0 en intergrant par parties.Je trouve 2-  mais je ne suis pas sure (c'est peu etre  -2)??? c'est là que ca commence a ce gaté 2. demontrer que la suite (In)est une suite géometreique dont on precisera la raison Q.Moi je voudrais bien calculer I(n+1)-In et donc je trouverais la raison mais le probleme c'est que je ne sais pas comment faire avec une divison d'integrale ??!! 3. On pose Sn= 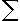 de n a k=0 de Ik . de n a k=0 de Ik .
Calculer Sn et determiner la limite de cette suite.et voila merci d'avance pour votre aide !! | |
|
  | |
R.O.G
Aidematheur



Nombre de messages : 471
Age : 36
Classe/Métier (si enseignant, précisez) : Professeur (stagiaire)
Localisation : Rennes
Loisirs : Sports d'endurance
Date d'inscription : 22/02/2008
 |  Sujet: Re: suite definie par une integrale Sujet: Re: suite definie par une integrale  Mar 18 Mar - 16:39 Mar 18 Mar - 16:39 | |
| Bonjour.Pour le 1) je trouve bien I0=  -2 //Plutôt I(0)=2-  //en cours de recherche de la suite (ai trouvé une méthode barbare et j'essaie de trouver mieux) //en cours de recherche de la suite (ai trouvé une méthode barbare et j'essaie de trouver mieux)
Dernière édition par R.O.G le Mar 18 Mar - 18:44, édité 2 fois (Raison : Erreur de calcul) | |
|
  | |
lachite
micro posteur

Nombre de messages : 25
Classe/Métier (si enseignant, précisez) : classe préparatoire PCSI
Date d'inscription : 31/10/2007
 |  Sujet: RE: Sujet: RE:  Mar 18 Mar - 17:53 Mar 18 Mar - 17:53 | |
| Merci pour votre aide mais j'ai un probleme car je n'arrive pas a trouver  -2 il faut que je remplace dans In les n par des zeros en faisant ça je trouve une integrale qui va de 0(dc en haut de l'integrale) a  (dc en bas) est ce que sa c'est juste ? puis je calcule normalement et je trouve : I0=1/2 [2xsin(x/2)+4cos(x/2)]0 est ce que c'est juste ? puis je calcule et je trouve : 1/2 ( (0+4)-(2*1+0)) et donc 2-  Mais en faisant comme ça je ne trouve pas comme vous ? je dois faire une erreur de calcul mais je n'arrive pas a la voir | |
|
  | |
R.O.G
Aidematheur



Nombre de messages : 471
Age : 36
Classe/Métier (si enseignant, précisez) : Professeur (stagiaire)
Localisation : Rennes
Loisirs : Sports d'endurance
Date d'inscription : 22/02/2008
 |  Sujet: Re: suite definie par une integrale Sujet: Re: suite definie par une integrale  Mar 18 Mar - 18:32 Mar 18 Mar - 18:32 | |
| Je n'avais pas lu l'intégrale ainsi ! (je croyais que c'était de 0 à  [c'est ainsi qu'on lit une intégrale, d'abord en bas puis en haut !]), Dans ce cas là, ton calcul doit être bon (le mien moins). | |
|
  | |
lachite
micro posteur

Nombre de messages : 25
Classe/Métier (si enseignant, précisez) : classe préparatoire PCSI
Date d'inscription : 31/10/2007
 |  Sujet: re: Sujet: re:  Mar 18 Mar - 18:35 Mar 18 Mar - 18:35 | |
| Désollé pour la confusion et merci pour ton aide | |
|
  | |
R.O.G
Aidematheur



Nombre de messages : 471
Age : 36
Classe/Métier (si enseignant, précisez) : Professeur (stagiaire)
Localisation : Rennes
Loisirs : Sports d'endurance
Date d'inscription : 22/02/2008
 |  Sujet: Re: suite definie par une integrale Sujet: Re: suite definie par une integrale  Mar 18 Mar - 18:42 Mar 18 Mar - 18:42 | |
| Pour la suite, j'ai calculé I(n) (pour tout n) par IPP. Pour montrer qu'elle est géométrique j'ai calculé I(n+1)/I(n) (ça donne la raison de la SG) //il faut dire avant que pour tout n In 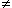 0). La dernière question est une question de 1° //il doit y avoir une solution plus simple... | |
|
  | |
lachite
micro posteur

Nombre de messages : 25
Classe/Métier (si enseignant, précisez) : classe préparatoire PCSI
Date d'inscription : 31/10/2007
 |  Sujet: re Sujet: re  Mar 18 Mar - 18:47 Mar 18 Mar - 18:47 | |
| mais comment tu fais pour calculer une divison d'intergrale ?? | |
|
  | |
R.O.G
Aidematheur



Nombre de messages : 471
Age : 36
Classe/Métier (si enseignant, précisez) : Professeur (stagiaire)
Localisation : Rennes
Loisirs : Sports d'endurance
Date d'inscription : 22/02/2008
 |  Sujet: Re: suite definie par une integrale Sujet: Re: suite definie par une integrale  Mar 18 Mar - 18:50 Mar 18 Mar - 18:50 | |
| Par définition, une intégrale est un nombre ! Tu calcules la valeur de In et I(n+1) et tu fais le rapport de ces 2 valeurs ! | |
|
  | |
lachite
micro posteur

Nombre de messages : 25
Classe/Métier (si enseignant, précisez) : classe préparatoire PCSI
Date d'inscription : 31/10/2007
 |  Sujet: re Sujet: re  Mar 18 Mar - 18:59 Mar 18 Mar - 18:59 | |
| okay et apres la qst 3. elle se fait grace a la reponse de la question 2 ? | |
|
  | |
R.O.G
Aidematheur



Nombre de messages : 471
Age : 36
Classe/Métier (si enseignant, précisez) : Professeur (stagiaire)
Localisation : Rennes
Loisirs : Sports d'endurance
Date d'inscription : 22/02/2008
 |  Sujet: Re: suite definie par une integrale Sujet: Re: suite definie par une integrale  Mer 19 Mar - 9:01 Mer 19 Mar - 9:01 | |
| Oui, Sn est somme d'une SG que tu peux exprimer en fonction de n et q. Ensuite, tu fais tendre n:fleche: + 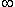 ! Voilà ! | |
|
  | |
lachite
micro posteur

Nombre de messages : 25
Classe/Métier (si enseignant, précisez) : classe préparatoire PCSI
Date d'inscription : 31/10/2007
 |  Sujet: re Sujet: re  Mer 19 Mar - 19:00 Mer 19 Mar - 19:00 | |
| Merci beaucoup j'ai reussi a repondre bon bien j'ai fini merci beaucoup pour ton aide !!  a+ | |
|
  | |
R.O.G
Aidematheur



Nombre de messages : 471
Age : 36
Classe/Métier (si enseignant, précisez) : Professeur (stagiaire)
Localisation : Rennes
Loisirs : Sports d'endurance
Date d'inscription : 22/02/2008
 |  Sujet: Re: suite definie par une integrale Sujet: Re: suite definie par une integrale  Mer 19 Mar - 20:55 Mer 19 Mar - 20:55 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: suite definie par une integrale Sujet: Re: suite definie par une integrale  | |
| |
|
  | |
| | suite definie par une integrale |  |
|





