Equations - exponentielle / logarithme

Bonsoir,

J'ai un problème avec un exercice.

Je dois résoudre ces 4 équations / inéquations :





Et je ne sais pas du tout comment m'y prendre

Si quelqu'un veut bien m'expliquer au moins comment commencer

Merci bien,

Bonne soirée

Jenilia

Bonsoir. Le truc à voir est

Puis en faisant le changement de variables

On essaie de finir l'exercie...
Voilà

Fiouu j'ai réussi à tout faire, pas sans mal mais bon ! Je suis contente, c'était pas si terrible que ça au final.

En tout cas Merci

Maintenant j'ai de gros problèmes avec les logarithmes. Je pense avoir besoin d'aide là aussi, pour commencer. Mais d'abord je réfléchis encore un peu devant mes exos, si je trouve vraiment pas j'reviendrais poster tout ça.

Me revoilà,

J'ai finalement pas mal avancé mais je suis complètement bloquée sur cet exercice :



Je comprend vraiment pas du tout du tout :s



Merci d'avance,

Jenilia

Commençons par la première question.

Il s'agit ici de trouver lambda tel que g vérifie l'équation différentielle (E)

Pour ce faire, remplace dans (E) y par g(x) et y' par g'(x)

En simplifiant l'expression ainsi obtenue, tu devrais pouvoir répondre à la première question

N'hésite pas à demander si tu ne comprends pas

Je trouve lambda = 2 4

Merci ; pour cette première question c'est compris

pour la deux,

f solution de (E) donc tu remplaces comme pour la une f dans (E) et on note cette équation (Ef)

de même g est solution (E) donc tu remplaces dans (E) et on note cette équation (Eg)

tu fais (Ef)-(Eg) et ensuite, tu devrais trouver le résultat

J'ai du faire une boulette quelque part :s

Je calcule (Ef)-(Eg), (Eg) se simplifie complètement donc
je trouve : f' = 4e^-2x - 3f

Donc f est bien solution de (E) mais h ? j'ai pas trop compris où il était passé celui là !

h = f-g, mais g se simplifie donc h = f ?
Et du coup y'a un problème pour ce qui est de l'équation (E') :s

Je suis un peu perdue ...

ok pas de stress ^^

f solution de (E) => f'(x)=-3f(x)+4e^(-2x) (Ef)
g solution de (E) => g'(x)=-3g(x)+4e^(-2x) (Eg)

Ainsi (Ef)-Eg) donne:

f'(x)-g'(x)=-3(f(x)-g(x))

On note h(x) = f(x) - g(x)

ainsi h'(x)=3h(x) donc h solution de (E')

Ahhh d'accord !!
Fallait pas remplacer g(x) par "lambda-etc" en fait.

J'ai compris,

Merci

Quelqu'un m'a mis un petit doute :

quand j'ai g(x) = lambda e^(-2x),
je dérive et j'obtiens g'(x) = -2 lambda e^(-2x)

et pas g'(x)= -2 e^(-2x) ?

oui parce que 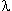est une constante :

dérivée de k*f c'est k*f' (pour t'en convaincre, tu fais k'f + kf' = kf' puisque dérivée d'une constante = 0)

Ah ouf

Merci beaucoup

Je vais garder ça dans un ptit coin de ma tête au cas où un doute refasse surface