| | algèbre: branches infinies |  |
|
|
| Auteur | Message |
|---|
souris bleue
petit posteur



Nombre de messages : 61
Localisation : quelque part en France (je ne veux pas dire la ville, c'est secret)
Loisirs : je fais de l'accordéon et de l'orgue
Date d'inscription : 02/11/2006
 |  Sujet: algèbre: branches infinies Sujet: algèbre: branches infinies  Jeu 4 Jan - 22:18 Jeu 4 Jan - 22:18 | |
|  Bonjour, pouvez-vous m'aidez pour l'exercice suivant? Je ne comprends pas très bien les questions surtout la première. Merci d'avance.  La fonction f est définie pour tout réel x par f(x)=e^(x/2)-(x/2)-1. On note C sa courbe représentative. 1) Etudier la branche infinie de C au voisinage de -∞ 2) Déterminer les limites de f(x) et de f(x)/x lorsque x tend vers +∞. C admet-elle une autre asymptote? 3) Déterminer la dérivée f' de f et établir le tableau de variation de f.
Dernière édition par le Sam 6 Jan - 14:11, édité 1 fois | |
|
  | |
St@rguill
Aidematheur



Nombre de messages : 149
Age : 37
Classe/Métier (si enseignant, précisez) : Ecole d'ingénieurs (Matméca-3ième année)
Localisation : Bordeaux (Talence)
Loisirs : Musique, Séries TV, Maths...
Date d'inscription : 10/06/2006
 |  Sujet: Re: algèbre: branches infinies Sujet: Re: algèbre: branches infinies  Ven 5 Jan - 1:51 Ven 5 Jan - 1:51 | |
| Pour la première question, je pense qu'il faut trouver la droite asymptote à C en - 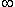 | |
|
  | |
souris bleue
petit posteur



Nombre de messages : 61
Localisation : quelque part en France (je ne veux pas dire la ville, c'est secret)
Loisirs : je fais de l'accordéon et de l'orgue
Date d'inscription : 02/11/2006
 |  Sujet: Re: algèbre: branches infinies Sujet: Re: algèbre: branches infinies  Sam 6 Jan - 1:30 Sam 6 Jan - 1:30 | |
| Coucou, pour la question1, j'ai fais l'étude de la branche infinie de C au voisinage de -∞.
On remarque que lim f(x) quand x tend vers -∞ est égale à +∞
On a aussi lin f(x)+x/2+1 quand x tend vers -∞ est égale à 0
Donc, f admet pour asymptote en -∞, la droite d'équation y= -x/2-1. Je voudrais savoir si c'est juste et, s'il faudrait rajouter quelque chose afin de vraiment répondre à la question 1.
Pour la question 2, j'ai trouvé que lim f(x) quand x tend vers +∞ est égale à +∞-∞ donc, c'est une FI après, je ne sais pas trop comment faire. Pour lim f(x)/x quand x tend vers -∞ du coup, je ne sais pas faire.
Pour la question 3, j'ai trouvé que f'(x)=(1/2)e^(x/2)-1/2. Par conséquent, j'ai trouvé à l'aide de la calculette que,f'x est négative sur [-∞;0] et positive sur [0;+∞]. Donc, f(x)d'abord décroissante puis croissante. Est-ce que cela est juste? | |
|
  | |
Shinichi
Adminimatheur



Nombre de messages : 2038
Age : 37
Classe/Métier (si enseignant, précisez) : Maitrise informatique
Localisation : Québec
Loisirs : bcp de choses
Date d'inscription : 04/02/2006
 |  Sujet: Re: algèbre: branches infinies Sujet: Re: algèbre: branches infinies  Sam 6 Jan - 1:40 Sam 6 Jan - 1:40 | |
| - souris bleu a écrit:
- 2) Déterminer les limites de f(x) et de f(x)/x lorsque c tend vers +∞.
C'est pas plutot x ? | |
|
  | |
St@rguill
Aidematheur



Nombre de messages : 149
Age : 37
Classe/Métier (si enseignant, précisez) : Ecole d'ingénieurs (Matméca-3ième année)
Localisation : Bordeaux (Talence)
Loisirs : Musique, Séries TV, Maths...
Date d'inscription : 10/06/2006
 |  Sujet: Re: algèbre: branches infinies Sujet: Re: algèbre: branches infinies  Sam 6 Jan - 2:17 Sam 6 Jan - 2:17 | |
| Pour la question 1, tu as raison, et ta justification est suffisante.
Pour la question 2, je ne sais pas si on te l'a dit, mais l'exponentielle l'emporte toujours sur la puissance en l'oo. En effet, l'exponentielle croit beaucoup plus vite que x, donc lim f(x) = +oo.
Pour la question 3, il faut justifier autrement qu'avec la calculatrice le signe de f'. Il faut pour cela résoudre l'équation : f'(x)=0 qui a une solution simple... | |
|
  | |
souris bleue
petit posteur



Nombre de messages : 61
Localisation : quelque part en France (je ne veux pas dire la ville, c'est secret)
Loisirs : je fais de l'accordéon et de l'orgue
Date d'inscription : 02/11/2006
 |  Sujet: Re: algèbre: branches infinies Sujet: Re: algèbre: branches infinies  Sam 6 Jan - 14:11 Sam 6 Jan - 14:11 | |
| - Shinichi a écrit:
- souris bleu a écrit:
- 2) Déterminer les limites de f(x) et de f(x)/x lorsque c tend vers +∞.
C'est pas plutot x ? oui, c'est bien x, je me suis trompée en écrivant  | |
|
  | |
souris bleue
petit posteur



Nombre de messages : 61
Localisation : quelque part en France (je ne veux pas dire la ville, c'est secret)
Loisirs : je fais de l'accordéon et de l'orgue
Date d'inscription : 02/11/2006
 |  Sujet: Re: algèbre: branches infinies Sujet: Re: algèbre: branches infinies  Sam 6 Jan - 14:13 Sam 6 Jan - 14:13 | |
| - St@rguill a écrit:
- Pour la question 1, tu as raison, et ta justification est suffisante.
Pour la question 2, je ne sais pas si on te l'a dit, mais l'exponentielle l'emporte toujours sur la puissance en l'oo. En effet, l'exponentielle croit beaucoup plus vite que x, donc lim f(x) = +oo.
Pour la question 3, il faut justifier autrement qu'avec la calculatrice le signe de f'. Il faut pour cela résoudre l'équation : f'(x)=0 qui a une solution simple... ok donc, pour la question 2, j'ai lim f(x) quand x tend vers +∞ est égale à +∞ lim f(x)/x quand x tend vers +∞ est égale à +∞ donc, je penses qu'il n'y a pas d'asymptote | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: algèbre: branches infinies Sujet: Re: algèbre: branches infinies  | |
| |
|
  | |
| | algèbre: branches infinies |  |
|





