Limite de fonction

Bonjour

J'ai un peu de mal avec les limites de fonctions et j'ai justement des questions dessus. Merci de pouvoir m'aider.

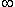
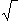
L'objet de l'exercice est l'étude complète de la fonction f définie sur [0; + [ par f(x) = (15-2x) (x ) +9x
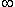
1) Déterminer la limite de f en + (je trouve que c'est une limite indéterminé mais je sais pas comment faire)

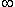
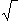
2) Soit g la fonction définie sur [ 0; + [ par g(x)= 18 (x) -6x+15
a) Déterminer la limite de g en +

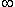
Merci

racine = puissance 1/2.

f(x) = 15*x^(1/2)-2*x^(3/2)+9*x donc la limite est -infini car le degré le plus grand est 3/2 et c'est "lui qui décide".

g-> -infini car -6 est le terme associé au terme de plus grand degré.