Exercice sur les barycentres

Bonjour, merci d'avance de votre aide sur cet exercice de barycentre

Matière / Niveau: 1ereS

Problème ou exercice:
Soit trois points de l'espace non alignes A,B,C et soit k un reel de l'intervalle [-1;1].
On note [tex]G_k[/tex] le barycentre du systeme {(A;[tex]k^2[/tex]+1)(B;k)(C;-k)}.

1) Montrer que pour tout reel k, le systeme admet un unique barycentre [tex]G_k[/tex]

2) Representer les points A,B,C, le milieu I de [BC] et construire les points [tex]G_1[/tex] et [tex]G-1[/tex]
(-1 est en indice)

3) Montrer que pour tout reel k de l'intervalle [-1;1] on a l'egalite
vect[tex]AG_k[/tex] =(-k)/(k^2+1)*[tex]vect{BC}[/tex]

4) A l'aide de votre calculatrice ou d'un grapheur comme GeoGebra, dresser le tableau de variation de la fonction f(x) = -x / (x^2 + 1)

5) En deduire l'ensemble des points [tex]G_k[/tex] lorsque k parcourt [-1;1]

Où j'en suis:

1) a + b + c = k^2 + 1 + k - k = k^2 + 1 different de 0
Pour tout reel k, le systeme admet donc un unique barycentre [tex]G_k[/tex]

2)
[tex]H_1[/tex] = bar {(A;2);(B;1)}
2H1A + H1B = 0
2H1B + 2BA + H1B = 0
3H1B = 2AB
H1B = 2/3 AB
BH1 = 2/3 BA
[tex]G_1[/tex] = bar{(H;3);(C;-1)}
3G1H - G1C = 0
3G1C + 3CH - G1C = 0
2G1C + 3CH = 0
2G1C = 3HC
2CG1 = 3CH
CG1 = 3/2 CH

[tex]H-1[/tex] = bar{(A;2);(B;-1)}
2H-1A - H-1B = 0
2H-1B + 2BA - H-1B = 0
H-1B = 2AB
BH-1 = 2BA

[tex]G-1[/tex] = bar {(H;1);(C;1)}
G-1H + G-1C = 0
G-1H + G-1H + HC = 0
2G-1H = CH
G-1H = 1/2CH
HG-1 = 1/2HC

Je n'en suis pas du tout sur...

3) Comment fait on ?

4) Tableau de valeurs

x------∝(negatif)-------1(negatif)----------1--------------------------+∝
f(x)-------fleche haut--0.5----fleche bas---0.5(negatif)--fleche haut

5) Pouvez vous m'expliquer?

Les balises TEX ne sont pas compatibles avec forumactif. Traduis d'abord l'écriture LaTeX et ensuite je t'aiderai.

Bonjour, merci d'avance de votre aide sur cet exercice de barycentre

Matière / Niveau: 1ereS

Problème ou exercice:
Soit trois points de l'espace non alignes A,B,C et soit k un reel de l'intervalle [-1;1].
On note G indice de k, le barycentre du systeme {(A;k^2+1)(B;k)(C;-k)}.

1) Montrer que pour tout reel k, le systeme admet un unique barycentre G indice de k

2) Representer les points A,B,C, le milieu I de [BC] et construire les points G indice de 1 et G indice de -1
(-1 est en indice)

3) Montrer que pour tout reel k de l'intervalle [-1;1] on a l'egalite
vectAG indice de k=(-k)/(k^2+1)*vectBC

4) A l'aide de votre calculatrice ou d'un grapheur comme GeoGebra, dresser le tableau de variation de la fonction f(x) = -x / (x^2 + 1)

5) En deduire l'ensemble des points G indice de k lorsque k parcourt [-1;1]

Où j'en suis:

1) a + b + c = k^2 + 1 + k - k = k^2 + 1 different de 0
Pour tout reel k, le systeme admet donc un unique barycentre G indice de k

2)
H indice de 1= bar {(A;2);(B;1)}
2H1A + H1B = 0
2H1B + 2BA + H1B = 0
3H1B = 2AB
H1B = 2/3 AB
BH1 = 2/3 BA
G indice de 1 = bar{(H;3);(C;-1)}
3G1H - G1C = 0
3G1C + 3CH - G1C = 0
2G1C + 3CH = 0
2G1C = 3HC
2CG1 = 3CH
CG1 = 3/2 CH

H indice de -1= bar{(A;2);(B;-1)}
2H-1A - H-1B = 0
2H-1B + 2BA - H-1B = 0
H-1B = 2AB
BH-1 = 2BA

G indice de -1= bar {(H;1);(C;1)}
G-1H + G-1C = 0
G-1H + G-1H + HC = 0
2G-1H = CH
G-1H = 1/2CH
HG-1 = 1/2HC

Je n'en suis pas du tout sur...

3) Comment fait on ?

4) Tableau de valeurs

x------∝(negatif)-------1(negatif)----------1--------------------------+∝
f(x)-------fleche haut--0.5----fleche bas---0.5(negatif)--fleche haut

5) Pouvez vous m'expliquer?

1-Soit k un réel appartenant à l'intervalle [-1;1], il n'existe dans cet intervalle aucune valeur de sorte de k²+1=0 puisque k² est toujours positif et que la somme de deux nombres réels positifs a pour résultat un nombre réel positif. Aussi, k²+1=0 n'a qu'une solution : k² = -1, or, c'est impossible.
Le barycentre existe donc.

//

Merci de votre aide mais je n'ai pas compris votre reponse sur la 2)
Avez vous fait un partie de l'exercice que j'avais fait faux ?

J'ai mis G au lieu de H (par simple habitude). Il s'agit du calcul du barycentre de (A;2)(B;1)

Mais dois je pas respecter les indices ? car ca remplace les k dans l'expression?

Si NON, C'est pas bete du tout !
C'est plus beau d'avoir un G que un H!!

L'indice du barycentre est en effet un réel k.

Pouvez vous m'expliquer la 3)

3) Montrer que pour tout reel k de l'intervalle [-1;1] on a l'egalite
vectAG indice de k=(-k)/(k^2+1)*vectBC

Par contre, si tu pouvais te servir du LaTeX ça rendrait ça beaucoup plus simple et beaucoup plus rapide à corriger. De plus, tu as déjà l'écriture LaTeX dans ton énoncé premier. Va sur le lien LaTeX. Il te suffira juste d'enlever les balises [tex][/tex].

Il n'y a pas de faux ni Juste

Je devais representer G indice de 1 et de indice de -1 !

3)(K^2+1)GA + kGB - kGC = 0
-(K^2+1)AG = kGC - kGB
-(K^2+1)AG = kGC - kGC - kCB
-(K^2+1)AG = kBC
AG = -k/(k^2+1) BC

Donc pour tout reel k de l'intervalle [-1;1] on a egalement l'egalite AG = -k/(k^2+1) BC


Est ce bon ?


Le tableau est comme ceci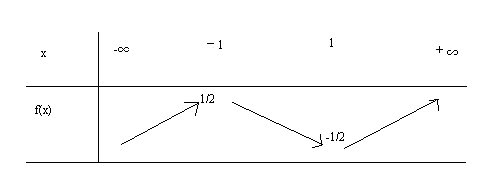


donc le 5) est

L'ensemble des points Gk lorsque k parcourt [-1;1] appartient a l'intervalle [-1/2;1/2]

L'énoncé est si bien écrit de façon explicite, ça ne m'étonne pas ...

Citation :

(K^2+1)GA + kGB - kGC = 0
-(K^2+1)AG = kGC - kGB
-(K^2+1)AG = kGC - kGC - kCB
-(K^2+1)AG = kBC
AG = -k/(k^2+1) BC

Quant au tableau de variation il n'est pas complet.

L'énoncé est si bien écrit de façon explicite, ça ne m'étonne pas ...　
Voulez vous dire que c'est bon ou c'est faux?

AH BON ? Que manque ' t il au tableau ?

Pouriez vous me dire que manque - t - il au tableau ! S'il vous plait!

//

Dsl je suis japonais donc je suis pas tres a l'aise avec le francais..
Voulez vous dire que vous aviez tort et vous etes trompe quand vous aviez fait la remarque car vous etiez fatigue?