| | Equation paramétrique |  |
|
|
| Auteur | Message |
|---|
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Equation paramétrique Sujet: Equation paramétrique  Mer 5 Nov - 18:58 Mer 5 Nov - 18:58 | |
| Zour la compagnie Après mon cher Shinichi m'ai laché  , je me permet de poster mon exercice sur les équa paramétrique... - Citation :
- On se place dans le plan orienté, muni d'un repère orthonormal direct (O,i,j).
POur tout réels x et y, on pose  . On note . On note 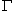 l'ensemble despoints du plan dont les coordonnées (x,y) vérifient F(x,y)=0 l'ensemble despoints du plan dont les coordonnées (x,y) vérifient F(x,y)=0
1. Soit t un réel, on note Dt l'ensemble des points du plan de coordonnées (x,tx) où x décrit 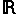
Identifier Dt. Déterminer Dt  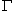
Pour tout t:appartient: 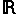 -{-1}, on pose -{-1}, on pose 
On note 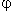 la courbe paramétrée par ( la courbe paramétrée par ( 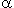 (t), (t), 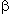 (t)), avec t décrivant (t)), avec t décrivant 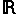 -{-1} -{-1}
2. comparer 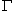 et et 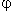 . On précisera si on a une égalité ou une simple inclusion. . On précisera si on a une égalité ou une simple inclusion.
3 étudier la courbe paramétrée 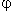 sur ]-1;1]. sur ]-1;1].
quelle transformation permet de contruire 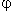 tout entière à partir de cette étude ? tout entière à partir de cette étude ?
4. étudier les branches infinies de 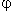
5. tracer l'allure de 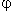
6 Donner une équation polaire de 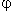 Alors je ne sais pas comment faire la 1 et la 2... pour la 3 j'imagine que ça en découle des deux questions précédentes (j'ai fait l'étude mais pas la transformation) pour la 4et5 c'est fait... La 6 je ne sais pas comment passer de l'équation cartésienne à la polaire... Pourriez vous me donner a méthode ? :/ Merci d'avance  | |
|
  | |
Redola
hyper posteur


Nombre de messages : 315
Age : 41
Classe/Métier (si enseignant, précisez) : ingénieur
Localisation : Lille
Date d'inscription : 28/09/2006
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Jeu 6 Nov - 21:42 Jeu 6 Nov - 21:42 | |
| pour la 1, il te suffit d'écrire la signification: Tu es dans R^2 Chaque point de Dt a pour absisse x, et pour ordonnée tx... Donc, Dt est un droite affine de coefficient directeur t... Pour l'intersection, écris les deux équation, cherche x en fonction de t et tu auras ta réponse  | |
|
  | |
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Jeu 6 Nov - 23:57 Jeu 6 Nov - 23:57 | |
| Donc si j'ai bien compris, on écrit :
x^3 + y^3 - 3xy = tx ?
Le soucis c'est qu'on a encore y O_o | |
|
  | |
Redola
hyper posteur


Nombre de messages : 315
Age : 41
Classe/Métier (si enseignant, précisez) : ingénieur
Localisation : Lille
Date d'inscription : 28/09/2006
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Ven 7 Nov - 0:02 Ven 7 Nov - 0:02 | |
| y=tx puisque le point appartient a Dt.. mais je ne suis pas d'accord avec ton équation en fait x^3 + y^3 - 3xy = 0 et y=tx et voila  | |
|
  | |
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Ven 7 Nov - 0:28 Ven 7 Nov - 0:28 | |
| Ahhh c'est tout con, j'étais parti sur un f(x) = tx moi >_<
Donc ça nous fais du x^3(t^3+1) - 3tx² = 0
x²(xt^3 + x - 3) = 0
donc x = 0
x = 3/(1+t^3)
C'est tout ? O_O | |
|
  | |
Redola
hyper posteur


Nombre de messages : 315
Age : 41
Classe/Métier (si enseignant, précisez) : ingénieur
Localisation : Lille
Date d'inscription : 28/09/2006
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Ven 7 Nov - 8:54 Ven 7 Nov - 8:54 | |
| tu as fait une erreur de calcul | |
|
  | |
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Ven 7 Nov - 9:08 Ven 7 Nov - 9:08 | |
| hummm mais j'ai réfléchit que puisque t parcours R... merci de ton aide, je vais mettre tout ça bien  | |
|
  | |
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Sam 8 Nov - 17:56 Sam 8 Nov - 17:56 | |
| humm c'est bon je m'en suis sorti, on trouvait la même chose que 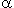 (t) (ou beta je sais plus)... Sinon, à propos des courbes paramétrées, quand on a des branches paraboliques, on a la direction (genre dirigée par Ox, etc...), comment on peut avoir l'équation de la parabole ? Dans un livre d'exo que j'ai, ils nous sortent 'la parabole d'équation truc', mais ils expliquent pas comment on trouve (ou alors très rapidement u_u")... Vous auriez la méthode, pour ma petite culture perso ? xD | |
|
  | |
Redola
hyper posteur


Nombre de messages : 315
Age : 41
Classe/Métier (si enseignant, précisez) : ingénieur
Localisation : Lille
Date d'inscription : 28/09/2006
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Lun 10 Nov - 12:03 Lun 10 Nov - 12:03 | |
| comme je le disais dans un message précédent, tout ce que je dis ici, je le fais uniquement de mémoire.... malheureusement, les courbes pamarétriques, je ne pratique vraiment pas souvent... donc, j'ai peu de souvenirs:(
Je ne peux malheureusement pas répondre à ta question... | |
|
  | |
Eximma
Adminimatheur



Nombre de messages : 1933
Age : 34
Classe/Métier (si enseignant, précisez) : mp
Localisation : St Nazaire (loire atlantique [44]) Mais Lorient en ce moment ^^
Loisirs : Plein de choseuhs
Date d'inscription : 15/12/2005
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  Lun 10 Nov - 21:35 Lun 10 Nov - 21:35 | |
| Ce n'est pas grave, merci pour ton aide quand même  Si shinichi passe pas là XD | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Equation paramétrique Sujet: Re: Equation paramétrique  | |
| |
|
  | |
| | Equation paramétrique |  |
|





