Dérivation et continuité.

Bonjour,

voici deux exercices de synthèse d'un de mes chapitres. Sachant que demain, j'ai un contrôle portant sur les dérivations, je vous demande de m'aider à faire ces exercices résumant l'ensemble de l'étude.

Voici le premier, N°75 :

Soit f une fonction définie sur [0;+inf[ par : f(x)= (x^3+x+3)/(1+x)²

1° Démontrer que f '(x)= (x^3+3x²-x-5)/(1+x)^3.

2° On pose la fonction g définie sur R par : g(x)= x^3+3x²-x-5 .

a) Déterminer le sens de variation de la fonction g, à l'aide de la dérivée.

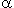
b) Montrer que l'équation g(x)=0 possède une solution dans [0;+inf[ ; en donnant la valeur décimale arrondie à 0.1 près.

c) En déduire le signe de g(x) sur [0;+inf[.

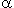
3° Déterminer le sens de variation de la fonction f. (on utilise la valeur trouvée précédemment).

4° Tracer la courbe représentative de la fonction f dans un repère orthogonal bien choisi.

Salut,

Pourrais tu nous dire ce que tu n'as pas réussi ?

Par exemple la dérivée et tout ça, c'est bon ? de même pou rle sens de variation ?

b) Montrer que l'équation g(x)=0 possède une solution dans [0;+inf[ ; en donnant la valeur décimale arrondie à 0.1 près.

c) En déduire le signe de g(x) sur [0;+inf[.

ces deux questions là, stp.

Salut !

La méthode pour ce genre de questions est la suivante :

On montre que sur [0;+inf[ g est strictement monotone (ie strict croissante ou strict décroissante) et continue (pas de soucis c'est une fonction polynomiale). Tu calcules les limites aux bornes de cette intervalle (ici en 0 = -5 et en +inf = + inf). Tu dis ensuite que g est donc une bijection de [0;+inf[ dans [-5;+inf[. Or 0 [-5;+inf[ donc l'équation g(x) = 0 admet bien une unique solution sur R+ (ici on la note ).

Pour trouver , comme on a pas d'indications ici, tu cherches avec ta calculatrice