Dérivation et continuité.

... et le N° 76 :

On considère la fonction f définie sur l'ensemble des réels strictement positifs par f(x)= (6/x)-(9/2x²)+(1/x^3).

Soit C la courbe représentative de la fonction f dans un repère orthonormal d'unités 3 cm.

1° Etudier les variations de f.
Dresser le tableau des variations, en précisant les extremums .

2° a) Résoudre l'équation f(x)=0.
En déduire que la courbe C ne traverse jamais l'axe des abscisses.

b) D'après le tableau des variations, discuter suivant les valeurs du réel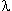
le nombre de solutions à l'équation f(x)= .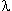

c) Construire les tangentes à la courbe C aux points d'abscisse (1/2) et 1. Tracer la courbe C.

Merci beaucoup pour vos réponses futurs.

b) D'après le tableau des variations, discuter suivant les valeurs du réel
le nombre de solutions à l'équation f(x)= .

c) Construire les tangentes à la courbe C aux points d'abscisse (1/2) et 1.

Pouvez vous m'aider à répondre à ces deux questions ? merci d'avance.

Bonjour,

Pour le 1- je suppose que tu n'as aucun souci pour établir un tableau de variations. Ca devrait ressembler à ça :


En 2- il faut résoudre l'équation f(x)=0. Pour cela, on a


Attention, il ne faut pas oublier de préciser que .

merci bien!

Souviens-toi de la définition d'une tangente à une courbe :
"Lorsqu'une courbe (C) est définie par son équation cartésienne de la forme y = f(x), les considérations permettent d'affirmer que si f est dérivable en xo, alors (C) admet une tangente au point M(xo,yo) qui a pour équation :

y - yo = y'o(x - xo) ou bien : y = y'o(x - xo) + yo avec y'o = f '(xo)"

ok merci

Je reviens rapidement au 2 -

merci sinon comment tu fais pour écrire comme ca ?

Je vais sur l'interface LaTeX. http://www.gnux.be/index.php?page=tex2im ou celle du forum http://sanu.evoconcept.net/FdM


Alors, tu me donnes les résultats que tu as trouvé pour la tangente et l'équation f(x)=0 ?