Bonjour
Voilà, j'ai un exercice à faire et je voudrais savoir si mes réponses sont bonnes car je n'arrive pas à faire tout l'exercice. Merci.
A(2;-1), B(8;-3), C(3;2), D(9;0) et E (6;1) sont des points du plan muni d'un repère orthonormal(O; vecteur i, vecteur j) et (C) le cercle d'équation: x²+y²-4x+2y-15=0. (Faire une figure que l'on complètera au fur et à mesure)
1) Déterminer une équation cartésienne de la droite (CD)
y=3x+18 (c'est ce que j'ai trouvé)
2)Déterminé le centre et le rayon du cercle (C). Montrer que E appartient au cercle C.
(C): (x-2)²+(y+1)²=20 (pour l'équation du cercle) donc centre (2;-1) et rayon 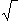 20
20
et j'ai trouvé que E appartenait au cercle (C)3) Déterminé une équation cartésienne du cercle (C') et de diamètre [AB]
Là je suis pas sur du tout. J'ai trouvé (C'): x²-10x+y²+4y=-19
4) Déterminé le ou les points d'intersection de (CD) et (C)
C'est à partir de là que je n'arrive pas, j'ai voulu faire un système mais ce que je trouve est vraiment bizarre voir impossible)
5) Déterminé le ou les points d'intersection de (C) et (C')
Je n'ai pas fait car je ne suis pas sur de mon équation de mon cercle (C')
6) Démontrer que (Cd) est tangente à (C')





